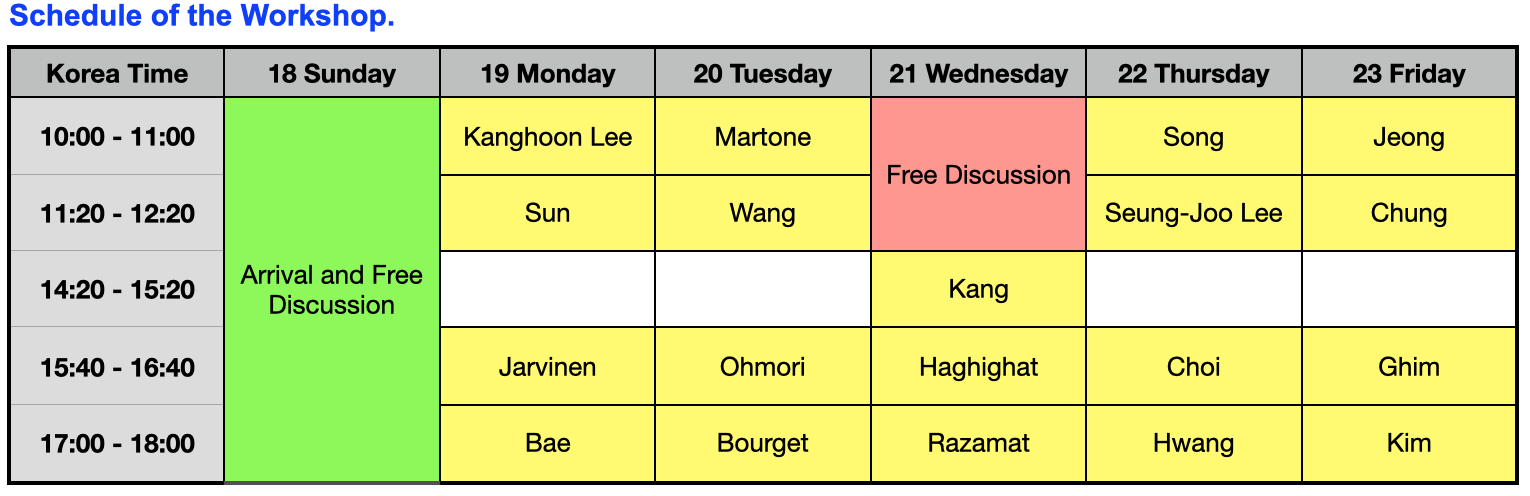
Time zone: Korea Stand Time (UTC/GMT+9 hours) 

 Talk Title

 Kanghoon Lee: Berends-Giele Recursion Relation for Gravity and Double Copy

 Kaiwan Sun: Blowup equations for quiver gauge theories

 Matti Jarvinen: Modeling neutron stars via gauge/gravity duality

 Jin-Beom Bae: Recent progress in fermionic rational conformal field theories

 Mario Martone: Characteristic dimension and isotrivial geometries.

In this talk I will provide an update on the classification program of 4d  SCFTs based on analyzing their moduli space geometries. After reminding the status of the two simplest cases, so-called rank-1 and rank-2, I will introduce novel techniques which will enable me to extend the classification to any rank. In particular I will introduce the characteristic dimension of an arbitrary 4d  SCFT, a simple quantity which can take only one out of eight rational values, and give the complete answer when the characteristic dimension is not 1 or 2.  

 Xin Wang: Elliptic quantum curves of 6d SO(N) theories

In this talk I will talk about recent developments on topological boundaries of 2+1d TQFTs. In particular about when such a boundary can exist. This talk will be based on an ongoing collaboration with Justin Kaidi, Zohar Komargodski, Sahand Seifnashri and Shu-Heng Shao.

In this talk I discuss how unitary quivers can be used to describe Higgs branches of certain 4d N=2 superconformal field theories. The geometry of the moduli space can be studied using the quiver subtraction algorithm, which involves elementary transverse slices in Affine Grassmannians. This is particularly rich in the case of non simply laced quivers, which are discussed in detail. The notion can also be extended to orthosymplectic quivers.

 Monica Jinwoo Kang: Approximation in infinite-dimensional entanglement wedge reconstruction.Approximation in infinite-dimensional entanglement wedge reconstruction

 Shlomo Razamat: Three road to the van Diejen model, and beyond 

 Babak Haghighat: Machine Learning the Kitaev Honeycomb model

 Jaewon Song: a vs c

 Seung-Joo Lee: On light towers of states at infinite distances

 Sunjin Choi: The Yang-Mills duals of small AdS black holes

 Chiung Hwang: Symmetry enhancement: from 4d mirror symmetry to E-string

 Saebyeok Jeong: Surface defects, spectral duality, and separation of variables

The four-dimensional N=2 supersymmetric field theories are associated with the integrable systems of Hitchin. For the class S theories for the Riemann sphere with regular punctures, the corresponding integrable system is most straightforwardly presented as the Gaudin system. Meanwhile, for special values of moduli it has been understood that there is a spectral duality between the Gaudin system and the XXX spin chain system. First, I will explain the insertion of half-BPS surface defects in the class S theory can be utilized to fully account for such a spectral duality. Then I will introduce how the quantum separation of variables for the integrable system can be constructed in this framework, interpreting it as a transition of M-branes which engineer the surface defect. Finally, I will explain the solutions to the spectral problem can be understood at the level of the hyper-Kahler geometry of the Hitchin moduli space. The talk is based on the upcoming paper with N. Lee and N. Nekrasov.

 Hee-Joong Chung: Resurgent analysis for knot invariants

 Dongwook Ghim: 5d BPS quivers and KK towers

This talk will present recent progress in computing (refined) Witten index of BPS quiver for 5d gauge theories, compactified on a circle. With stringy BPS objects in 5d theory being wrapped on the circle, the wall-crossing problem of 4d KK theory can be addressed by N=4 quiver quantum mechanics. However, the fine-tuned superpotential of the latter makes many of the known machinery fail to capture its Witten indices. I will show how the subtlety can be bypassed for a restricted class of BPS quivers. Specifically, I will construct the entire KK tower of Cartan components in vector multiplets, based on L2 cohomology counting and D0 brane picture. Time permitting, the analysis will be extended to purely electric BPS particles in the weak coupling chamber.

 Jung-Wook Kim: Is the hidden symmetry of Schwarzschild spacetime anomalous?